Minimum Spanning Trees - Kruskal’s Algorithm
Minimum Spanning Trees - Kruskal’s Algorithm
Spanning Trees
One of the concepts I found really interesting in a recent Data Mining course was that of Minimum Spanning Trees. A Spanning Tree is a type of Proximity Graph where all nodes of the graph are connected but there are no loops or cycles created.
A Spanning Tree has n-1 edges, where n is the number of nodes. A Minimum Spanning Tree (MST) is a subset of a Spanning Tree that selects edges from the graph such that all nodes are connected and the total weight of the selected edges is minimised.
Minimum Spanning Tree
An MST is used to show the connections between the nodes of a proximity graph and, since it’s a minimum total edge weight, it will show the smallest or closest connections aspart of the resultant graph.
MST Algorithms
There are a number of different algorithms for calculating an MST, two of these are:
Both of these two algorithms are greedy (Prim’s is greedy by nodes and Kruskal’s is greedy by edges). Kruskal’s algorithm is the one that is used in the code below and this works by first ordering all the edges from smallest to largest edge weight. The smallest edge weights are then joined together (unless they form any loop or cycle) until a complete tree has been created.
Example
Having a quick look back at the previous example in my proximity graph generator post, the output proximity graph for this is not a spanning tree as not all nodes are connected. Therefore, the MST generated for this example shows the minimum connections for the large, interconnected group.
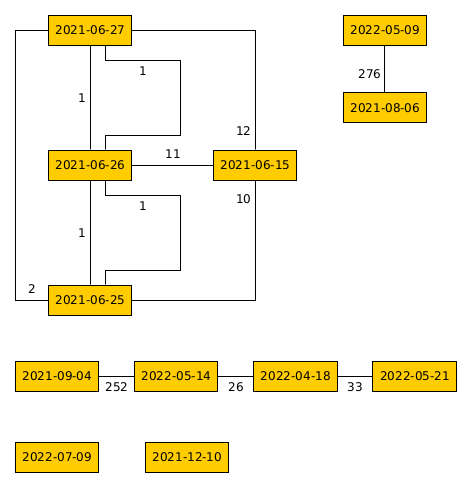 Original proximity graph
Original proximity graph
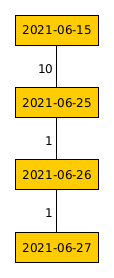 MST
MST
Kruskal’s Algorithm in Python
Whilst studying this, I found the GeeksForGeeks tutorial for Kruskal’s Algorithm in Python 1 on this very helpful and used this code myself. Whilst using it I updated the code slightly to use variables that aligned with the course materials that I was using, added some comments to help me understand each section (the union and ranking part took a little while for my head to process), and added in debugging sections throughout.
The debugging sections are definitely not an ideal way of doing this and, if I end up reusing this later on, I’d probably change how this is implemented.
Kruskal’s algorithm in Python
class MSTGraph:
def __init__(self, vertices, debug=False):
self.vertices = vertices
self.graph = []
self.debug = debug
self.result = []
def add_edge(self, u, v, w):
self.graph.append([u, v, w])
# Parent search function
def get_parent(self, parent, vertex):
# If the parent of the current vertex is the current
# vertex, then the parent has been found
if parent[vertex] == vertex:
return vertex
# If not, then call the find function again, but this time
# with the parent of the original 'vertex' variable used
return self.get_parent(parent, parent[vertex])
# This function creates the connections between vertices. The Union is between
# the two vertices current being added
def apply_union(self, parent, rank, x, y):
xroot = self.get_parent(parent, x)
yroot = self.get_parent(parent, y)
# DEBUG INFO
if self.debug:
print(f'Parent before: {parent}')
print(f'Rank before: {rank}')
# Checks the rank list and picks the vertex with the highest
# rank to be the parent of the union
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
else:
parent[yroot] = xroot
rank[xroot] += 1
# DEBUG INFO
if self.debug:
print(f'Parent after: {parent}')
print(f'Rank after: {rank}')
# Applying Kruskal algorithm
def mst_kruskal(self):
# Initialise the loop counter, i, and the
# number of edges, e, to 0
i, mst_edges = 0, 0
# Sort the graph by the 3rd (index 2) value of each list
self.graph = sorted(self.graph, key=lambda item: item[2])
parent = []
rank = []
# For loop creates the lists for both parent and rank
# and initialises the parent to each node as a subset
# of itself, and rank is initialised to all 0's
for node in range(self.vertices):
parent.append(node)
rank.append(0)
# Main routine
while mst_edges < self.vertices - 1:
# DEBUG INFO
if self.debug:
print(f'\nStep {i}\n')
print(f'Current MST has {mst_edges} edges and is: {self.result}')
u, v, weight = self.graph[i]
i += 1
x = self.get_parent(parent, u)
y = self.get_parent(parent, v)
# DEBUG INFO
if self.debug:
print(f'u\'s ({u}) parent is {x}')
print(f'v\'s ({v}) parent is {y}')
if x != y:
mst_edges += 1
self.result.append([u, v, weight])
self.apply_union(parent, rank, x, y)
# Print the resultant MST
# DEBUG INFO
if self.debug:
print(f'Finished MST is {self.result}')
edge_weight_total = 0
for u, v, weight in self.result:
edge_weight_total += weight
return edge_weight_total
def get_vertices(self):
vertices = []
for vertex in self.result:
if vertex[0] not in vertices:
vertices.append(vertex[0])
if vertex[1] not in vertices:
vertices.append(vertex[1])
vertices = sorted(vertices, key=lambda item:item)
return vertices
def get_edges(self):
edges = []
for edge in self.result:
edges.append((edge[0], edge[1]))
return edges
def get_weights(self):
weights = []
for weight in self.result:
weights.append(weight[2])
return weights